• • About
  • Algorithms
  • Results
  • Code
  • Home

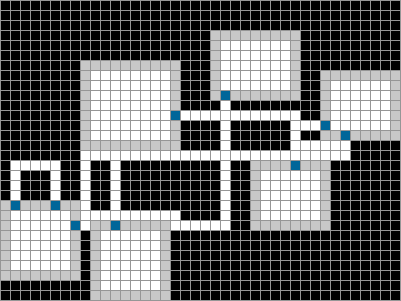
Procedural content generation is a great way to generate interesting worlds, and dungeon generation is often the first step in level creations. A variety of algorithms have been researched and developed to produce interesting random levels that make games, especially roguelike games, unique and fun.

Procedural Cave

The project initially began around July of 2010 as a simple excercise to generate random caves and dungeons procedurally. Months later, some of this program's code was used in while working on a game's level generator. As the dungeon generator grew and more algorithms were added, the generator was split off as a stand-alone system capable of creating nice dungeons using a variety of methods.

Below is the original prototype cave generator, which procedurally "grows" a cave based on user inputs. To create a new cave, press Enter.

The dungeon generation code is very modular, so it should be very easy to add new dungeon algorithms. The program creates a grid in the form of a 2D array and passes it to the dungeon algorithm, which then modifies that array. Too add a new algorithm, just create a new file with your new code and pass the array to it.

Algorithms

Several algorithms are implemented; some are very simple while others contain complex data structures and pathfinding algorithms. Read on for an explanation of each algorithm, or go to the end to look at the results, as well as downloads and the source code.

Random Room Placement

One of the most simple and probably the most used dungeon algorithm. This method places rooms randomly on the grid, then loops over each room and attempts to connect them. If given the chance, random tunnels can also be dug out to give the dungeon a more natural feel. The steps are as follows:

1. Determine the number of rooms to be created based on the room layout selected, and updates various user-configured variables in updateParam()
2. Calls initRooms() to create a room of random width and height at a random location on the grid. A random number of openings (doors) are placed on the room's walls.
3. Check if the room is outside of the grid or blocked by another room or corridor through blockRoom(). If blocked, delete the room and repeat step 2.
4. After all rooms are initialized, call initCorridors() to connect the openings in each room. In basicAStar(), A* pathfinding is used to look for the optimal path from one door to another. Weights are used so that the corridors are more likely to be straight and join each other.
5. If there are any openings left unconnected, randomly tunnel corridors out from the opening by calling tunnelRandom(), if the corridor reaches a room wall, add a door there.

Different types of dungeons can be generated based on minimum and maximum room size and the number of rooms. The A* algorithm uses the Manhattan method to calculate its heuristics, and a Binary Heap is used to store the nodes.

References:
- pcg.wikidot.com/pcg-algorithm:dungeon-generation
- donjon.bin.sh/dungeon/about/
- www.policyalmanac.org/games/aStarTutorial.htm

Cellular Automata

Based on the cellular automata method by Jim Babcock, this algorithm uses cellular automaton to create natural-looking caves. Usually cellular automation uses the 4-5 rule: a tile becomes a wall if it was a wall and 4 or more of its nine neighbors were walls, or if it was not a wall and 5 or more neighbors were. This algorithm is a slightly modified version of that logic:

Tile T will be filled if either
- T is already filled *and* at least 4 of its neighbors are filled
- T is not yet filled *and* at least 5 of its neighbors are filled

This is the same thing as sayin
Tile T will be filled if the number of tiles within one step of T, including T itself, is at least 5.

But this is not the function which my sample program uses. The function I use is
Tile T will be filled if the number of tiles within one step of T, including T itself, is at least R1Cutoff OR the number of tiles within TWO steps of T, including T itself, is at MOST R2Cutoff.

So, if R1Cutoff=4 and R2Cutoff=5, that will happen almost all of the time.

Anyways, the function I eventually chose as the 'best' answer was
Fill: 40%
Repeat 4 times:
    R1 cutoff: 5
    R2 cutoff: 2
Repeat 3 times:
    R1 cutoff: 5
    R2 cutoff: -1

So the parameters would be
xsize ysize 40 5 2 4 5 -1 3

So, it first fills the grid randomly with walls and empty cells, then goes over each grid cell and applies the following rules to the cell:

1. A tile T becomes a wall if 5 or more of the tiles within one step of T are walls.
2. A tile T becomes a wall if 2 or less of the tiles within two step of T are walls.

Repeat that three times, and the user gets a somewhat natural-looking cave. To clean up the cave further and reduce the number of disconnected caves, the loop is run for four more iterations, except this time a tile T becomes a wall if 5 or more of the tiles within one step of T are walls, and becomes a wall if none of the tiles within two step of T are walls.

Do note that although the second iteration lowers the possibility of disjointed caves, it may still happen.

References:
- www.jimrandomh.org/misc/caves.html
- pixelenvy.ca/wa/ca_cave.html

BSP Tree

This is an algorithm that takes advantage of a tree data structure called BSP tree to make sure there are no overlapping rooms during dungeon generation. The algorithm itself is fairly straightforward, as outlined below (check here for a more visual explanation):

1. Start with a rectangular dungeon.
2. Choose a random direction (horizontal or vertical) and location (x for vertical or y for horizontal).
3. Split the dungeon into two sub-dungeons using the parameters obtained in step 2.
4. Pick a random sub-rectangle and repeat step 2 for n iterations.
5. After n iterations, place random sized rooms in each of the rectangles.
6. Connect each room by looping through all the split rectangles and connect each split sub-regions.

References:
- www.roguebasin.com/index.php?title=Basic_BSP_Dungeon_generation
- stackoverflow.com/questions/4997642/simple-example-of-bsp-dungeon-generation

Procedurally Build

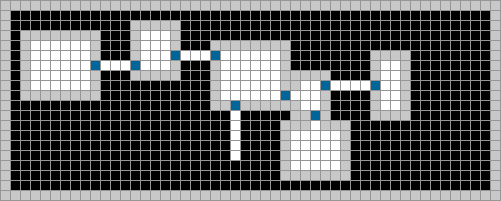
Based on the method described by Mike Anderson, this is another fairly simple algorithm, and one that most resemble how an actual dungeon is built. The algorithm first generates a room in the center of the grid, then connects more rooms and corridors to the room and newly placed elements. In effect, the dungeon "grows" outward from the center room:

1. Fill the whole map with solid earth
2. Dig out a single room in the centre of the map
3. Pick a wall of any room
4. Decide upon a new feature to build
5. See if there is room to add the new feature through the chosen wall
6. If yes, continue. If no, go back to step 3
7. Add the feature through the chosen wall
8. Go back to step 3, until the dungeon is complete

The original code tends to create rooms connected to rooms with dead end corridors sticking out, this version is modified to reduce the number of dead ends and increase the likelihood of a room being generated at the end of a corridor.

This algorithm is implemented to test the extensibility of the dungeon generator, efforts were made to retain as much of the original code as possible.

References:
- www.roguebasin.com/index.php?title=Dungeon-Building_Algorithm
- www.roguebasin.com/index.php?title=Java_Example_of_Dungeon-Building_Algorithm
- openprocessing.org/visuals/?visualID=18822

Results

The program should be fairly straightforward to use. Press 'space' to generate new dungeons, play around with the parameters and see how they affect the dungeon created. Click 'Save' to save the current dungeon to a file.

Download the generator for your system of choice: