Volumetric Clouds
A Volume Renderer that Utilizes Ray Casting and Ray Marching through a 3D Voxel Grid to Generate Puffy Clouds
Originally finished in 2009, this program first reads a text file containing initialization variables, then uses those variables to create a voxel grid data structure and uses ray marching to read lighting and density information from the grid in order to render fluffy clouds. The program was updated in 2010: the code was completely rewritten to improve efficiency, several new algorithms were implemented for voxel grid traversal, Perlin Noise was implemented to generate random clouds, and a GUI was created to make it more user-friendly (for the few users that actually stumble across it, that is).
Features
- Generates volumetric clouds with ray marching on a voxel density grid
- Trilinear interpolation to produce more realistic results
- Random cloud generator using Perlin noise
- Can read in custom-made cloud configuration files or output current cloud as a new configuration file
- GUI that allows the user to move the camera and see rendering progress
- Optimized for faster speed
Voxel Grid
A voxel grid is a NxNxN grid of voxels where each voxel stores properties such as density, color, and transmissivity. The voxel class can take any world-space coordinate and transform it into local voxel-space coordinate. Each voxel is stored in a vector array, and can be access through a function that translates x, y, z coordinates into array indices (index = x + y*(number of x voxel) + z*(number of x voxel)*(number of y voxel)). Arbitrary values are picked to break a tie in the case of a ray hitting the very edge between two voxels.
The voxel grid class also includes a default density (0 in this case). The default density's main purpose is to provide a density value when given coordinates outside the grid, which can happen to voxels at the edge of the grid during trilinear interpolation.
Ray Marching
Similar to raytracing, a ray has a beginning point P and a direction V. The ray marching algorithm was tested in a series of unit tests by moving along the ray in both discrete and uniform steps. While "marching" through voxels, the ray reads the voxel's properties such as density, which is then used in calculating lighting and density accumulation.
Several optimizations were made to the ray march algorithm. Instead of marching a ray from the viewport to the grid, the ray starts at the grid's edge. Also, the march will stop as soon as the ray finds itself outside the grid.
Different algorithms can be implemented to produce different (and sometimes better) results. The original ray march algorithm simply takes one step each iteration, where a step is the length of either one or half of a voxel:
1: // Ray Marching
2: while (ray is inside grid) {
3: points.push_back(orig); // Stores the point
4: orig = orig + step*dir; // Increment step
5: }
6:
However, if the step size is too large, the ray may miss a voxel completely (and thus missing the rendering properties for that block), but decreasing the step size too much and rendering will slow to a crawl. One solution is to check for all voxels that the ray passes through by running a ray-cube intersection test on all voxels. Unfortunately the speed of this method is also not satisfactory. We can further improve performance by choosing which voxel to test for intersection (for a 3D grid, at each step there can only be 3 possible voxels that the ray intersects next). In the end, keep in mind that intersection test itself can be very slow, so if we have a large grid with many voxels, the number of intersection test alone will take up a lot of time.
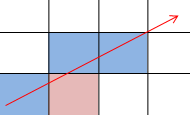
Another solution is Bresenham's line rasterization algorithm. The algorithm can determine which points in an n-dimensional raster should be plotted in order to form a close approximation to a straight line between two given points. The algorithm is often used to draw lines on a computer screen, code for the 2D cases is fairly straightforward to implement, and can be easily extended to the 3rd dimension. However, Bresenham's algorithm is not adequate for our purpose, since the set of pixels that are detected does not include all pixels through which the line passes. In the image below, the ray passes through the red grid but it is overlooked.
So what to do? Amanatides and Woo to the rescue! In the paper A Fast Voxel Traversal Algorithm for Ray Tracing, Amanatides and Woo present a solution to this problem by finding the minimum of the x and y distance (and in our case z as well) where the ray crosses over the current voxel boundary. The paper even comes with pseudocode of the algorithm. There are also several good resources online that provide examples of the initialization part of the algorithm:
- www.clockworkcoders.com/oglsl/rt/gpurt3.htm (Recommended)
- www.ray-tracing.ru/articles182.html
- www.mathworks.com/matlabcentral/fileexchange/26852
- devmaster.net/posts/2836/raytracing-theory-implementation-part-1-introduction
Keep in mind that this algorithm can also be slow if you have too many voxels, since each and every voxel the ray passes through is processed. Using this method, the resulting clouds are generally darker than outputs from regular ray marching due to the fact no voxels are skipped, resulting in more opacity being accumulated during ray casting. Due to the fact that the algorithm stops at the edge of each voxel, when doing trilinear interpolation, all the weights end up being the same, giving less-than-ideal results:
The left image is produced using regular ray marching with trilinear interpolation, the right image is produced using voxel-by-voxel marching with trilinear interpolation.
Illumination and Precomputing Transmittance
Each step through the voxel grid involves an illuminance calculation Q(), which in turn involves another ray march through the voxel grid towards the light. This step simply finds the full transmittance from the point in question to the light, by casting from that point to the point of light. This ray march has the same step size as the other ray march.
Pre-computed transmittance is added to improve performance. Before rendering, a new voxel grid with the same size/shape as the density grid is created with the transmittance (Q) value calculated and stored in each cell. During rendering, the stored Q value is used rather than performing an extra ray march to gather illumination.
Volumetric Rendering
A ray is cast along the line of sight between the eye point (viewport) and each pixel to accumulate the opacity and color. The ray stops when transmittance becomes close to 0, or the ray leaves the grid. In the latter case, the resulting value is then blended with the background color to provide the color of that pixel. The full accumulation algorithm is as follows:
1: for each point along the ray { 2: color = colorAtPoint*lightColor; // Color 3: deltaT = exp(-kapa*stepSize*densityAtPoint); // Kapa is a constant 4: T *= deltaT; // Transmittance 5: 6: // When transmittance becomes close to zero we stop 7: if (T < 1e-6) 8: break; 9: 10: // Rendering equation 11: color += (1 - deltaT)/kapa*color*T*precomputedTransmittance; 12: } 13: 14: pixel = color + backgroundColor*T; 15:
Trilinear Interpolation
Trilinear interpolation is used to improve the quality of the renderings. To get a better picture of how it works, look at the following two images from Wikipedia:
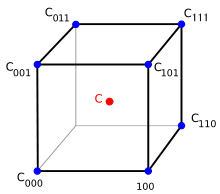
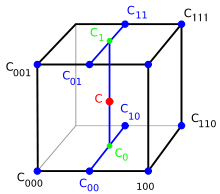
In our case, we use it to express ray march position as a weighted sum of voxel positions (a bit different from the above method):
1: // Tri-linear interpolation
2: for (k = z; k <= z + 1; k++)
3: for (j = y; j <= y + 1; j++)
4: for (i = x; i <= x + 1; i++)
5: weightx = (voxelSize - |x - i*voxelSize|)/voxelSize;
6: weighty = (voxelSize - |y - j*voxelSize|)/voxelSize;
7: weightz = (voxelSize - |z - k*voxelSize|)/voxelSize;
8:
9: weight = weightx*weighty*weightz;
10: interpolatedDensity += weight*VoxelDensityAt(ii, jj, kk);
11:
Cloud Generator and Perlin Noise
This generates voxel grids by filling a density grid with variables that produce good-looking clouds. Perlin noise is used to generate density values at each voxel with respect to a general spherical shape. Maximum size of the grid is also needed to ensure the generated cloud don't touch the boundary of the grid (or it will look like the cloud is cut off).
Below are several good references for Perlin noise and how to use it to create realistic-looking clouds:
- http://freespace.virgin.net/hugo.elias/models/m_perlin.htm (Recommended)
- http://freespace.virgin.net/hugo.elias/models/m_clouds.htm (Especially on CloudCover and CloudSharpness)
- http://www.sepcot.com/blog/2006/08/PDN-PerlinNoise2d
- http://www.flipcode.com/archives/Perlin_Noise_Class.shtml (A Perlin noise class)









